Magnetic flux and magnetic flux density
What are magnetic flux and magnetic flux density?
Magnetic flux is the magnetic flux density that runs through an imagined surface, with the magnetic flux density referring to the density of the field lines. The denser the field lines are, the greater the magnetic flux density. Since, according to the physical laws of electrodynamics, Maxwell's equations, no field lines can simply stop, the flux density continues to run from the magnet into the outside space.Table of Contents
What do the magnetic flux and magnetic flux density indicate?
The magnetic flux Φ can be understood as the totality of all magnetic field lines. The magnetic flux density B describes the density and direction of the field lines that pass through an imagined surface in space. If the field lines run in a straight line (for example between the poles of a horseshoe magnet), then the magnetic flux Φ through a certain area A, which is perpendicular to the flux, is the product of the magnetic flux density B and the area A: Φ = B•AIndirectly, the magnetic flux density (B field) is also a measure of the strength of the magnetic field. However, it is not entirely correct to refer to the B field itself as a magnetic field, even if this is occasionally found in the literature. The magnetic field is usually abbreviated with the letter H and the relationship B=μ0 μ•H with the magnetic permeability constant of the vacuum µ0 and a material-specific magnetic permeability constant µ applies. However, it is usually around 1, except for ferromagnetic materials, for which µ can assume values of up to 100 000 and for superconductors where µ=0. The product of µ,µ0 and magnetic field H results in the B field, i.e. the magnetic flux density B.
The magnetic flux density is measured in tesla (T). The magnetic flux correspondingly in Tm². The unit 1 Tm² is also referred to as 1 weber (Wb).
The remanence of a magnetised material is the magnetic flux density that emanates from the material after magnetisation. It is also given in tesla.
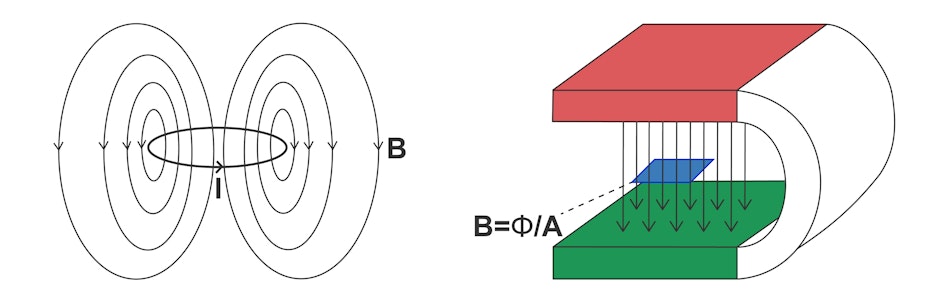
Illustration: A current I
always causes a magnetic flux density B.
A magnetic flux emanates from a circular current, which surrounds the conductor loop in the manner shown.
The field lines are drawn schematically.
In reality, the magnetic flux fills the entire space, and the field lines are always closed as a whole.
They run in the outside space from the north pole to the south pole and then through the conductor loop from the south pole to the north pole.
In the horseshoe magnet (right-hand side, north pole red, south pole green), they run back to the north pole within the material.
It does not matter for the course of the field lines whether we are talking about a magnetic flux density B
or a magnetic field H,
as both are proportional to each other.
The relationship B=μ0μ•H
applies.
As shown on the right-hand side, the magnetic flux density is the proportion of the magnetic flux Φ
per area A
(shown in blue).
B
is therefore proportional to the number of field lines that pass through an imagined surface.
Currents as a cause
Magnetic flux is caused by currents, i.e. by the movement of charges. Currents will always create closed field lines. The magnetic flux, therefore, has no beginning and no end. Or, if you want to put it in physics terms, there are no sources and sinks of magnetic flux density and magnetic flux.This, in turn, is the reason why a magnet must always have two poles: a north pole and a south pole. Mathematically, this is expressed by Maxwell's equations. An electromagnet is a typical current-driven magnet.
In permanent magnets, too, microscopic circular currents I, namely movements of the electrons in the material, are responsible for the magnetic flux and thus also for the magnetic field. These circular currents cause a magnetic flux B, which emerges from the circular current (current loop), runs in an arc to the underside of the current loop and closes again there (cf. illustration). The circular current creates a magnetic moment with the north pole above the conductor loop and the south pole below the conductor loop. If the direction of the current is reversed, the north and south poles are also swapped.
Determining the magnetic flux
Accordingly, the magnetic flux is physically defined by its inductive effect on a conductor loop. If a conductor loop with a known area is placed in a magnetic field, a voltage surge is induced. The time integral over this voltage surge is equal to the magnetic flux Φ:\(\int{U_{ind}dt}=B\cdot{A}=\Phi\)
Using a conductor loop and the voltage induced in this conductor loop, the magnetic flux can therefore also be measured. However, a more precise Hall probe is usually used for this purpose.
Determining the magnetic flux density
If you consider the magnetic flux density B, which runs through a curved surface, the magnetic flux must be determined as the integral of the vectorial flux density over the surface normal:\(\int{\vec{B}d\vec{A}}=\Phi\)
Since the field lines are closed, all field lines passing outwards through a closed surface (e.g. a spherical shell) must also pass back into the sphere and vice versa. In mathematical terms, this means that the flux through closed surfaces is always zero and, equivalently, there are no sources or sinks of magnetic flux density:
\(\oint_{A-geschlossen}{\vec{B}d\vec{A}}=0 \Leftrightarrow \vec{\nabla}\cdot{\vec{B}}=0\)
This is equivalent to the so-called freedom from divergence of the magnetic flux density, as stated by one of Maxwell's four equations.
In our FAQ section, you will find a table in Excel or OpenOffice format that you can use to conveniently calculate the flux density of magnets.

Author:
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
The copyright for all content in this compendium (text, photos, illustrations, etc.) remains with the author, Franz-Josef Schmitt. The exclusive rights of use for this work remain with Webcraft GmbH, Switzerland (as the operator of supermagnete.pt). Without the explicit permission of Webcraft GmbH, the contents of this compendium may neither be copied nor used for any other purpose. Suggestions to improve or praise for the quality of the work should be sent via e-mail to
[email protected]
© 2008-2024 Webcraft GmbH
© 2008-2024 Webcraft GmbH